PrimeGenerator - Clean code vs Philosophy 2
Tento článek je pokračováním Clean Code vs Philosophy of software design. V minulém článku jsem rozebíral chyby, které dělal Uncle Bob a John Ousterhout při implementaci PrimeGeneratoru. V tomto článku předvedu moji implementaci.
Kdo je čtenář kódu?
Počítám s tím, že čtenář kódu není matematik nebo člověk se znalostí generování prvočísel. Moje představa je, že píšeme třeba běžný Eshop a vedení se z nějakého podivného důvodu rozhodlo v prvočíselné dny nabídnout slevu.
Pokud bychom byli matematici, tak bych předpokládal hlubší znalosti matematiky a nepsal bych tolik komentářů.
Matematika za kódem
Moje implementace začíná následujícím komentářem:
// This is an implementation of incremental sieve of Eratosthenes with many optimizations.
// To understand this code you need to first understand incremental sieve of Eratosthenes.
// Incremental version is not commonly used so there are not many good resources describing it.
// I have created internal document [link] which describes it. !!STUDY IT FIRST!!Odkaz v tomto komentáři by vedl na samostatný dokument v gitu nebo na interní wiki a obsahoval by následující informace:
Interní dokument - Incremental Sieve of Eratosthenes
Abychom mohli pochopit, jak funguje Incremental Sieve of Eratosthenes, musíme nejprve pochopit, jak funguje Sieve of Eratosthenes.
Sieve of Eratosthenes
Sieve of Eratosthenes je algoritmus, který najde všechna prvočísla na daném intervalu - int[] Sieve(int from, int to). Například pro from=2 a to=10 vrátí pole [2, 3, 5, 7].
Příklad fungování pro interval 2-10:
- Vytvořte pole všech čísel v daném intervalu (číslo 1 ignorujte).
- [2, 3, 4, 5, 6, 7, 8, 9, 10]
- Vezměte první číslo z intervalu a uložte ho do výsledného pole prvočísel.
- 2
- Odstraňte z pole toto číslo a všechny jeho násobky.
- [3, 5, 7, 9]
- Opakujte kroky 2-3, dokud pole není prázdné.
- další číslo z pole je 3
- odstranění násobků - [5, 7]
- další číslo z pole je 5
- odstranění násobků - [7]
- další číslo z pole je 7
- odstranění násobků - []
Výsledkem je pole prvočísel - [2, 3, 5, 7].
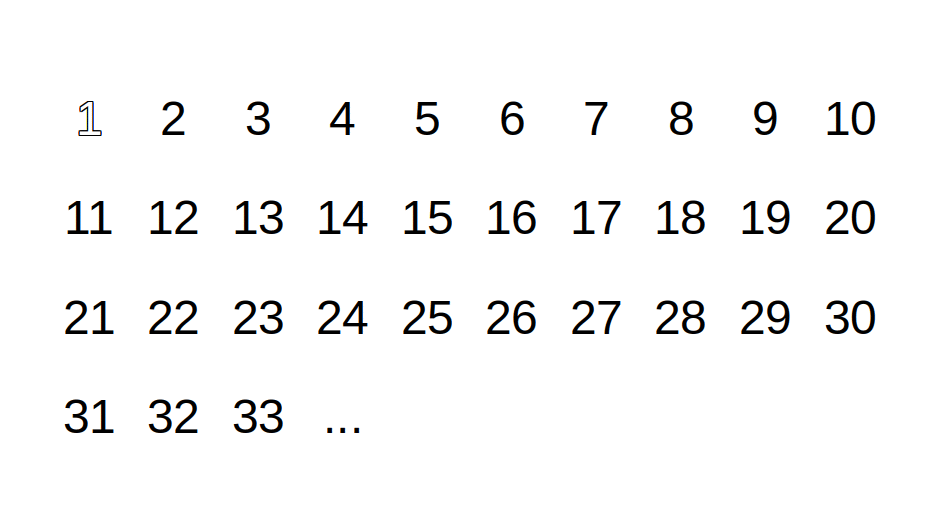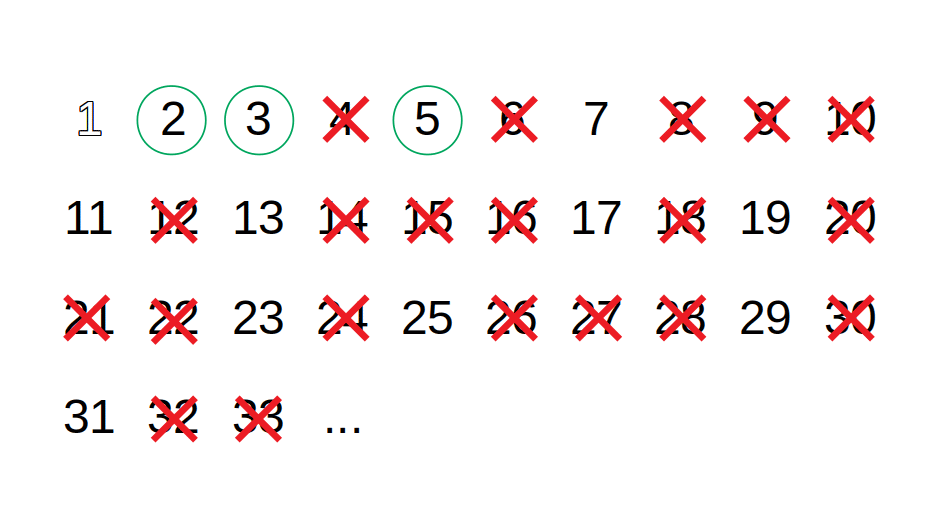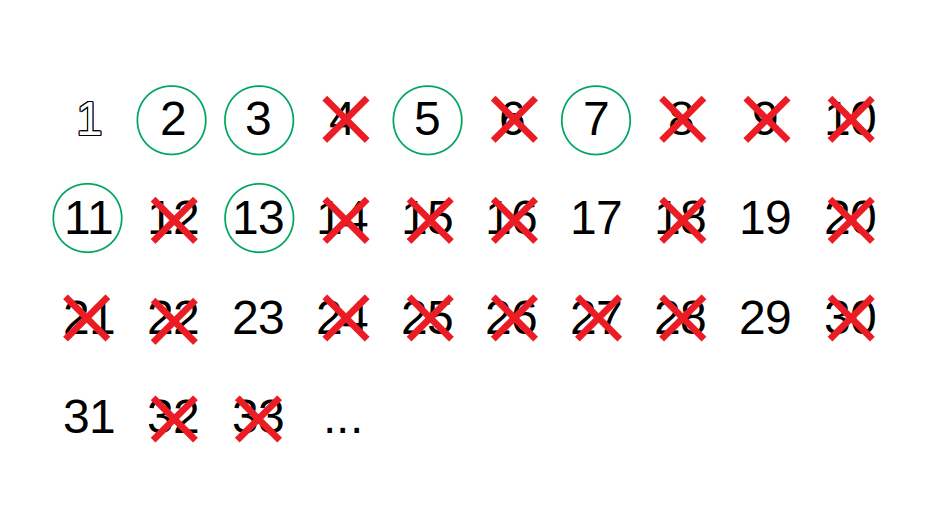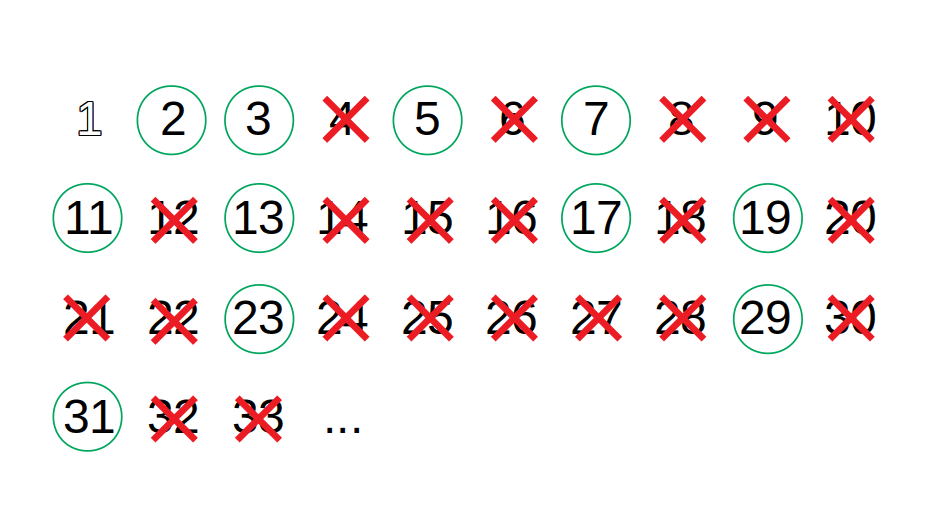
Incremental Sieve of Eratosthenes
Incremental Sieve funguje odlišně - na vstupu máme počet prvočísel, které chceme najít - int[] GeneratePrimes(int numberOfPrimesToGenerate). Například pro numberOfPrimesToGenerate=5 vrátí pole [2, 3, 5, 7, 11].
Pro vysvětlení fungování potřebujeme 2 proměnné:
candidateForPrime- číslo, u kterého zkoumáme, zda je prvočíslem.multiplesOfPrimes- obsahuje prvočísla a jejich násobky; je to pole objektů[(prime: 2, multiple: 4), (prime: 3, multiple: 6), ...]
Algoritmus pak funguje tak, že se snaží zjistit, zda candidateForPrime je obsažen v hodnotách multiple v poli multiplesOfPrimes. Pokud tam je, tak candidateForPrime není prvočíslo, a pokud tam není, tak candidateForPrime je prvočíslo.
Nyní už je otázkou pouze to, jak ukládat nové násobky do multiplesOfPrimes. K tomu nám pomůže následující ukázka:
Na začátku nastavíme multiplesOfPrimes = [] a spustíme algoritmus:
- Je
2prvočíslo?- Obsahuje
multiplesOfPrimes[].multiplečíslo2? multiplesOfPrimesobsahuje[]- žádný zmultiplese nerovná 2, takže 2 je prvočíslo.- Do
multiplesOfPrimespřidáme(prime: 2, multiple: 4)- 4 je první násobek dvojky (2*2).
- Obsahuje
- Je
3prvočíslo?- Obsahuje
multiplesOfPrimes[].multiplečíslo3? multiplesOfPrimesobsahuje[(prime: 2, multiple: 4)]- žádný zmultiplese nerovná 3, takže 3 je prvočíslo.- Do
multiplesOfPrimespřidáme(prime: 3, multiple: 6)- 6 je první násobek trojky (3*2).
- Obsahuje
- Je
4prvočíslo?- Obsahuje
multiplesOfPrimes[].multiplečíslo4? multiplesOfPrimesobsahuje[(prime: 2, multiple: 4), (prime: 3, multiple: 6)]- 4 je obsaženo vmultiple, takže 4 není prvočíslo.- Zvyš násobek všude, kde
multiple == 4- tedy(prime: 2, multiple: 4)se mění na(prime: 2, multiple: 6)(4 + prime).
- Obsahuje
- Je
5prvočíslo?- Obsahuje
multiplesOfPrimes[].multiplečíslo5? multiplesOfPrimesobsahuje[(prime: 2, multiple: 6), (prime: 3, multiple: 6)]- žádný zmultiplese nerovná 5, takže 5 je prvočíslo.- Do
multiplesOfPrimespřidáme(prime: 5, multiple: 10)- 10 je první násobek pětky (5*2).
- Obsahuje
- Je
6prvočíslo?- Obsahuje
multiplesOfPrimes[].multiplečíslo6? multiplesOfPrimesobsahuje[(prime: 2, multiple: 6), (prime: 3, multiple: 6), (prime: 5, multiple: 10)]- 6 je obsažena vmultiple, takže 6 není prvočíslo.- Inkrementuj
multiplesOfPrimesvšude, kdemultiple == 6- tedy(prime: 2, multiple: 6)se mění na(prime: 2, multiple: 8)a(prime: 3, multiple: 6)se mění na(prime: 3, multiple: 9)(6 + prime).
- Obsahuje
- …
Obecné fungování algoritmu:
Nalezení prvočísla:
- Vezmeme
candidateForPrime. - Pokud žádný z
multiplesOfPrimes[].multipleneobsahujecandidateForPrime, tak jecandidateForPrimeprvočíslo. - Do
multiplesOfPrimespřidáme kandidáta a jeho první násobek(prime: candidateForPrime, multiple: candidateForPrime * 2). - Zvýšíme
candidateForPrimeo 1 a pokračujeme bodem 1.
Nenalezení prvočísla:
- Vezmeme
candidateForPrime. - Pokud jeden nebo více
multiplesOfPrimes[].multipleobsahujecandidateForPrime, takcandidateForPrimenení prvočíslo. - Všude, kde se v
multiplesOfPrimes[].multiplenacházícandidateForPrime, zvýšíme hodnotumultiplesOfPrimes[x].multipleomultiplesOfPrimes[x].prime. - Zvýšíme
candidateForPrimeo 1 a pokračujeme bodem 1.
Optimalizace
Teď když víte, jak funguje Incremental Sieve of Eratosthenes, můžete se podívat na další část komentáře v kódu, která popisuje optimalizace:
// Optimizations used in this algorithm
// Optimization 1:
// When we find a prime, we set its entry in multiplesOfPrimes to prime * prime, instead of prime * 2.
// Why can we do this? Let's say we have found 5 as a prime.
// We set its first multiple to 5 * 5 = 25. We don't need 5*2, 5*3, 5*4 because all of them
// will be found as multiples of smaller primes - 2, 3, 2 (yes 2, not 4, because 4 is not prime).
// Optimization 2:
// We check only odd numbers – this is obvious because even numbers (except 2) cannot be prime.
// Optimization 3:
// We start with 2 as the first prime and 4 as the first multiple of 2. We skip the check for number 2.
// Optimization 4:
// We don't check all multiples in the multiplesOfPrimes array because it's not necessary.
// For example - we have multiplesOfPrimes = [4, 9, 25] and are checking if 7 is prime.
// We only need to check if 7==4 and 7==9 to determine if 7 is prime. We don't need to check 7==25 because we know that
// 9 > 7 and therefore all subsequent entries in multiplesOfPrimes are also greater than 7.
// Optimization 5:
// We don't use an array of prime-multiple pairs like [(prime: 2, multiple: 4)]. Instead, we use two separate arrays:
// For example, foundPrimes[0] is 2, and its multiple is stored in multiplesOfPrimes[0].
// So for prime "foundPrimes[x]" always has it's multiples in multiplesOfPrimes[x].
// Further optimizations:
// There are further, less complicated optimizations which are not described here.Celá implementace
Všimněte si, že komentář metody nepoužívá XML (Javadoc), ale obyčejný komentář. Je to proto, že text je určen pro člověka, který chce podrobně pochopit algoritmus, a ne pro někoho, kdo ho chce pouze použít.
Prime Generator
public static class PrimeNumberGenerator
{
// This is an implementation of incremental sieve of Eratosthenes with many optimizations.
// To understand this code you need to first understand incremental sieve of Eratosthenes.
// Incremental version is not commonly used so there are not many good resources describing it.
// I have created internal document [link] which describes it. !!STUDY IT FIRST!!
//
// Optimizations used in this algorithm
// Optimization 1:
// When we find a prime, we set its entry in multiplesOfPrimes to prime * prime, instead of prime * 2.
// Why can we do this? Let's say we have found 5 as a prime.
// We set its first multiple to 5 * 5 = 25. We don't need 5*2, 5*3, 5*4 because all of them
// will be found as multiples of smaller primes - 2, 3, 2 (yes 2, not 4, because 4 is not prime).
// Optimization 2:
// We check only odd numbers – this is obvious because even numbers (except 2) cannot be prime.
// Optimization 3:
// We start with 2 as the first prime and 4 as the first multiple of 2. We skip the check for number 2.
// Optimization 4:
// We don't check all elements of the multiplesOfPrimes array because it's not necessary.
// For example - we have multiplesOfPrimes = [4, 9, 25] and are checking if 7 is prime.
// We only need to check if 7==4 and 7==9 to determine if 7 is prime. We don't need to check 7==25 because we know that
// 9 > 7 and therefore all subsequent entries in multiplesOfPrimes are also greater than 7.
// Optimization 5:
// We dont use array of primes and multiples `[(prime: 2, multiple: 4)]`. Instead, we use two separate arrays:
// `foundPrimes = [2]` and `multiplesOfPrimes = [4]`.
// This is because we know that the index of the prime in `foundPrimes`
// is the same as the index of its first multiple in `multiplesOfPrimes`.
// For eample - `foundPrimes[0]` is 2 and it's multiples are saved in `multiplesOfPrimes[0]`.
// Further optimizations:
// There are further, less complicated optimizations which are not described here.
public static int[] Generate(
int numberOfPrimesToGenerate)
{
if (numberOfPrimesToGenerate <= 0)
{
throw new ArgumentException(
"Number of primes to generate must be greater than 0.",
nameof(numberOfPrimesToGenerate));
}
// We know how many primes we will generate, so we can preallocate.
var foundPrimes = new int[numberOfPrimesToGenerate];
// Multiples also never exceed the number of primes we will find because they are multiples of the found primes.
var multiplesOfPrimes = new int[numberOfPrimesToGenerate];
// This is used for an optimization later on - we don't need to check all multiples of primes.
var indexOfLastMultipleWhichWeHaveToCheck = 0;
// The first prime is always 2.
foundPrimes[0] = 2;
// First multiple is always 2 * 2 = 4.
multiplesOfPrimes[0] = 4;
// We have already found 2 as the first prime.
var numberOfPrimesFound = 1;
// The first candidate is always 3. We set this to 1 because it will be immediately incremented to 3.
var candidateForPrime = 1;
while (numberOfPrimesFound < numberOfPrimesToGenerate)
{
// We know that even numbers (except 2) cannot be prime, so we skip them.
candidateForPrime += 2;
// This is an optimization - we don't need to check all multiples of primes.
// For example - we have multiplesOfPrimes = [4, 9, 25] and are checking if 7 is prime.
// We only need to check if 7==4 and 7==9 to determine if 7 is prime. We don't need to check 7==25 because we know that
// 9 > 7 and therefore all subsequent entries in multiplesOfPrimes are also greater than 7.
indexOfLastMultipleWhichWeHaveToCheck = AdjustIndexOfLastMultipleWhichNeedToBeChecked(
candidateForPrime,
multiplesOfPrimes,
indexOfLastMultipleWhichWeHaveToCheck);
// Check if the candidate is a multiple of any of the previously found primes
// and increase the multiplesOfPrimes array if necessary.
var isCandidatePrime = AdjustMultiplesOfPrimesAndCheckTheCandidate(
candidateForPrime,
multiplesOfPrimes,
indexOfLastMultipleWhichWeHaveToCheck,
foundPrimes);
if (!isCandidatePrime)
{
continue;
}
foundPrimes[numberOfPrimesFound] = candidateForPrime;
// Set the multiple of the prime - we use the square of the prime as an optimization.
// See Optimization 1 for details.
multiplesOfPrimes[numberOfPrimesFound] = candidateForPrime * candidateForPrime;
numberOfPrimesFound++;
}
return foundPrimes;
}
private static bool AdjustMultiplesOfPrimesAndCheckTheCandidate(
int candidateForPrime,
int[] multiplesOfPrimes,
int indexOfLastMultipleWhichWeHaveToCheck,
int[] foundPrimes)
{
for (var i = 0; i < multiplesOfPrimes.Length; i++)
{
// First element contains multiples of 2.
// We can skip these because we skip even candidatesForPrime.
if (i == 0)
{
continue;
}
// We don't need to check all multiples, as an optimization.
if (i > indexOfLastMultipleWhichWeHaveToCheck)
{
break;
}
// We need to increment all smaller multiples before we can check if the candidate is prime.
// Example - candidate is 11 and multiplesOfPrimes = [4, 9, 25, 49] from primes (2, 3, 5, 7).
// We increment 9 by its prime - 9 + 3 = 12.
// (This is a theoretical example for 9; multiples of 2, like 4, are skipped by the i==0 check).
multiplesOfPrimes[i] = IncrementMultipleUntilItsLargerThenCandidate(
multiplesOfPrimes[i],
candidateForPrime,
// This is another optimization.
// For example, for prime 3, without this optimization, we would increment by 3: 9, 12, 15, 18, 21, 24.
// But 12, 18, 24 are useless because they are even, and we only check odd candidates.
// With increment 2 * foundPrimes[i], we get for prime 3: 9, 15, 21, 27, 33, 39 - all relevant (odd) multiples.
// It works for all odd (>2) primes (it's a neat mathematical trick).
increment: 2 * foundPrimes[i]);
// Check if the candidate is present in multiplesOfPrimes.
if (multiplesOfPrimes[i] == candidateForPrime)
{
return false;
}
}
return true;
}
private static int IncrementMultipleUntilItsLargerThenCandidate(
int multiple,
int candidateForPrime,
int increment)
{
var newMultipleValue = multiple;
while (newMultipleValue < candidateForPrime)
{
newMultipleValue += increment;
}
return newMultipleValue;
}
private static int AdjustIndexOfLastMultipleWhichNeedToBeChecked(
int candidateForPrime,
int[] multiplesOfPrimes,
int numberOfMultiplesWhichWeHaveToCheck)
{
var result = numberOfMultiplesWhichWeHaveToCheck;
if (candidateForPrime >= multiplesOfPrimes[numberOfMultiplesWhichWeHaveToCheck])
{
result++;
}
return result;
}
}Jaké změny jsem provedl?
Kromě přidání popisu algoritmu jsem provedl ještě několik úprav, které podle mě zlepšují čitelnost kódu. Pojďme se na nejdůležitější rozdíly podívat.
Rozdělení do metod
Ústředním tématem diskuse Boba i Johna je, zda kód rozdělit do metod, nebo ne. Osobně jsem zvolil rozdělení kódu do menších metod, ale na rozdíl od Boba jsem se snažil, aby čtenář byl schopen kód pochopit i bez toho, aby musel zkoumat obsah jednotlivých metod.
Dále jsem se snažil vyhýbat globálnímu kontextu, ke kterému mají přístup všechny metody (tak jak to má Uncle Bob). Jsem velký fanoušek pure funkcí a snažím se čtenáři ukázat všechny vstupy i výstupy metod vždy, když je to možné.
Pojmenování proměnných
Upravil jsem názvy proměnných:
| Uncle Bob | John Ousterhout | Moje verze |
|---|---|---|
primesFound | primesFound | numberOfPrimesFound |
primes | primes | foundPrimes |
n | n | numberOfPrimesToGenerate |
primeMultiples | multiples | multiplesOfPrimes |
lastRelevantMultiple | lastMultiple | indexOfLastMultipleWhichWeHaveToCheck |
V některých případech jsem se v kódu Johna i Boba ztrácel právě kvůli názvům - například název n pro počet hledaných prvočísel je velice nešťastný, jelikož si celou dobu musíte pamatovat, co n znamená.
primes a primesFound je taky poměrně matoucí - první je pole již nalezených prvočísel a druhé je počet nalezených prvočísel.
Hlavní for cyklus
Oba autoři používají tento for cyklus pro nalezení prvočísel:
for (int candidate = 3; primesFound < n; candidate += 2) { Osobně se snažím vyhýbat for cyklům, jejichž podmínka (primesFound < n) vůbec nesouvisí s inkrementací (candidate += 2) a inicializací (int candidate = 3). Podmínku je podle mého názoru lehké přehlédnout.
Z tohoto důvodu jsem upravil kód následujícím způsobem:
// The first candidate is always 3. We set this to 1 because it will be immediately incremented to 3.
var candidateForPrime = 1;
while (numberOfPrimesFound < numberOfPrimesToGenerate)
{
candidateForPrime += 2;Kontrola na prvočísla v samostatné metodě
Kontrolu na prvočísla jsem přesunul do samostatné metody AdjustMultiplesOfPrimesAndCheckTheCandidate. Kdyby kód nebyl extrémně optimalizovaný, tak bych udělal 2 smyčky - jednu pro AdjustMultiplesOfPrimes a druhou pro CheckCandidateForPrime. Jelikož ale řešíme optimalizovaný kód, tak jsem vytvořil jednu metodu, která používá and, i přes to, že and v názvech metod je kontroverzní.
Druhá věc, která je trochu zavádějící, je, že metoda AdjustMultiplesOfPrimesAndCheckTheCandidate upravuje pole multiplesOfPrimes. Kdybych psal neoptimalizovaný kód, tak bych vrátil nové pole multiplesOfPrimes a neupravoval původní. Abych alespoň částečně upozornil čtenáře na skutečnost, že je pole upravováno, tak jsem název metody obrátil z CheckTheCandidateAndAdjustMultiplesOfPrimes na aktuální název AdjustMultiplesOfPrimesAndCheckTheCandidate.
Vnořená smyčka
Pro vnořenou smyčku John i Bob používají:
for (int i = 1; i <= lastMultiple; i++) {Tento kód jsem upravil na:
for (var i = 0; i < multiplesOfPrimes.Length; i++)
{
// First element contains multiples of 2.
// We can skip those because we skip even candidatesForPrime.
if (i == 0)
{
continue;
}
// We don't need to check all multiples as an optimization.
if (i > indexOfLastMultipleWhichWeHaveToCheck)
{
break;
}ze 2 důvodů:
- Je jednoduché přehlédnout, že se iteruje od 1 a ne od 0.
- V neoptimalizovaném algoritmu se iteruje přes celé pole
multiplesOfPrimes. Iterace po proměnnouindexOfLastMultipleWhichWeHaveToCheckje pouze optimalizací. Myslím si, že můj kód na tuto skutečnost poukazuje lépe než kód Johna a Boba.